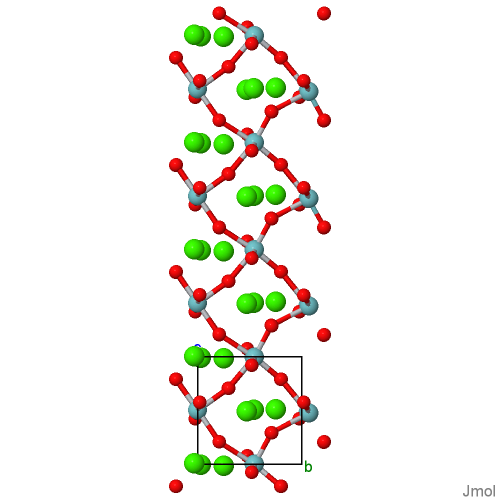
Superspace description of the crystal structures of Can(Nb,Ti)nO(3n+2) (n=5 and 6)
Authors:Guevarra, Jonathan; van Smaalen, Sander; Schonleber, Andreas; Lichtenberg, Frank
Journal:Acta Crystallographica, Section B 63 183-189 (2007)
DOI:https://doi.org/10.1107/S0108768107002340
B-IncStrDB ID: 5MeJVfvDRPN Entry date: 2022-01-25 Last revision: 2022-01-25
Ca5_Nb4_Ti_O17
Chemical data
Structural Formula Sum: Ca3.333 Nb2.666 O11.333 Ti0.667 [ Help ]
Formula weight: 594.5 Da [ Help ]
Crystallographic data and experimental details
Crystal system: monoclinic [ Help ]
Superspace group name: C'21/d(σ1σ20)-10 [ Help ]
Symmetry operations of the superspace group: (Show/hide table) [ Help ]
| Operation code | Operation in algebraic form |
|---|---|
| 1 | x1,x2,x3,x4 |
| 2 | -x1,-x2,-x3,1/2-x4 |
| 3 | 1/4-x1,-x2,1/2+x3,1/4-x4 |
| 4 | x1,1/2+x2,1/2-x3,x4 |
| 5 | 1/2+x1,x2,x3,1/2+x4 |
| 6 | 1/2-x1,-x2,-x3,-x4 |
| 7 | 3/4-x1,-x2,1/2+x3,3/4-x4 |
| 8 | 1/2+x1,1/2+x2,1/2-x3,1/2+x4 |
| 9 | 3/4+x1,1/2+x2,x3,1/4+x4 |
| 10 | 3/4-x1,1/2-x2,-x3,3/4-x4 |
| 11 | -x1,1/2-x2,1/2+x3,1/2-x4 |
| 12 | 3/4+x1,x2,1/2-x3,1/4+x4 |
| 13 | 1/4+x1,1/2+x2,x3,3/4+x4 |
| 14 | 1/4-x1,1/2-x2,-x3,1/4-x4 |
| 15 | 1/2-x1,1/2-x2,1/2+x3,-x4 |
| 16 | 1/4+x1,x2,1/2-x3,3/4+x4 |
a: 7.6889(3) Å [ Help ]
b: 5.3381(3) Å [ Help ]
c: 5.47630(10) Å [ Help ]
α: 90 ° [ Help ]
β: 90 ° [ Help ]
γ: 89.921(4) ° [ Help ]
Volume: 224.770(16) Å3 [ Help ]
Z: 1 [ Help ]
Modulation dimension: 1 [ Help ]
Measured independent wave vectors: (Show/hide table) [ Help ]
| Wave vector id | q_x | q_y | q_z |
|---|---|---|---|
| 1 | 0.00000 | 0.08333 | 0.00000 |
μ: 5.867 mm-1 [ Help ]
Absorption correction type: none [ Help ]
Minimum transmission factor: 1.000 [ Help ]
Maximum transmission factor: 1.000 [ Help ]
Refinement details
Total nb. of reflections: 3231 [ Help ]
Nb. of observed reflections: 2731 [ Help ]
Intense reflections threshold: I>3σ(I) [ Help ]
Refinement based on: F [ Help ]
R(all): 0.0583 [ Help ]
R(obs): 0.0512 [ Help ]
wR(obs): 0.0600 [ Help ]
wR(all): 0.0614 [ Help ]
S(all): 2.63 [ Help ]
Nb. of reflections: 3231 [ Help ]
Nb. of parameters: 146 [ Help ]
Weighting scheme: sigma [ Help ]
Weighting scheme remarks: w=1/(σ2(F)+0.0001F2) [ Help ]
Δ/σ(max): 0.0048 [ Help ]
Δ/σ(mean): 0.0003 [ Help ]
Δρ(max): 3.02 e_Å-3 [ Help ]
Δρ(min): -2.65 e_Å-3 [ Help ]
Extinction method: none [ Help ]
Structural Information
Average Structure: (Show/hide table) [ Help ]
| Atom symbol | Atom site label | x | y | z | Uiso/equiv | ADP type | Coords from (d)iffraction or (c)alculated | Coords restraints or constraints | Occupancy | Disordered cluster | Disordered group |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ca | Ca1 | -0.00010(10) | -0.03459(17) | 0.00495(14) | 0.0107(3) | Uani | d | . | 0.125 | . | . |
| Ca | Ca2 | 0.00186(16) | 0.3304(2) | -0.0818(2) | 0.0087(3) | Uani | d | . | 0.0417 | . | . |
| Ca | Ca3 | -0.00721(17) | -0.2504(3) | 0.0136(3) | 0.0159(4) | Uani | d | . | 0.0417 | . | . |
| Nb | Nb11 | 0.25 | 0 | 0.5 | 0.00382(16) | Uani | d | . | 0.167(7) | . | . |
| Ti | Ti11 | 0.25 | 0 | 0.5 | 0.00382(16) | Uani | d | . | 0.041(7) | . | . |
| Nb | Nb12 | 0.25 | 0 | 0.5 | 0.00382(16) | Uani | d | . | 0.144(7) | . | . |
| Ti | Ti12 | 0.25 | 0 | 0.5 | 0.00382(16) | Uani | d | . | 0.022(7) | . | . |
| Nb | Nb13 | 0.25 | 0 | 0.5 | 0.00382(16) | Uani | d | . | 0.078(7) | . | . |
| Ti | Ti13 | 0.25 | 0 | 0.5 | 0.00382(16) | Uani | d | . | 0.005(7) | . | . |
| Nb | Nb21 | 0.75 | 0 | 0.5 | 0.00388(16) | Uani | d | . | 0.172(7) | . | . |
| Ti | Ti21 | 0.75 | 0 | 0.5 | 0.00388(16) | Uani | d | . | 0.036(7) | . | . |
| Nb | Nb22 | 0.75 | 0 | 0.5 | 0.00388(16) | Uani | d | . | 0.148(15) | . | . |
| Ti | Ti22 | 0.75 | 0 | 0.5 | 0.00388(16) | Uani | d | . | 0.019(15) | . | . |
| Nb | Nb23 | 0.75 | 0 | 0.5 | 0.00388(16) | Uani | d | . | 0.079(15) | . | . |
| Ti | Ti23 | 0.75 | 0 | 0.5 | 0.00388(16) | Uani | d | . | 0.004(15) | . | . |
| O | O1 | -0.0001(2) | 0.0137(3) | 0.5794(4) | 0.0069(6) | Uani | d | . | 0.2083 | . | . |
| O | O2 | 0.2145(2) | 0.2118(3) | 0.2060(3) | 0.0073(5) | Uani | d | . | 0.25 | . | . |
| O | O3 | 0.7864(2) | 0.1989(3) | 0.1976(4) | 0.0077(5) | Uani | d | . | 0.25 | . | . |
ADP components: (Show/hide table) [ Help ]
| Atom site label | U11 | U22 | U33 | U12 | U13 | U23 | Atom site symbol |
|---|---|---|---|---|---|---|---|
| Ca1 | 0.0094(5) | 0.0123(4) | 0.0105(5) | 0.0001(3) | -0.0003(3) | -0.0032(3) | Ca |
| Ca2 | 0.0057(6) | 0.0117(6) | 0.0088(6) | -0.0006(5) | -0.0002(6) | -0.0013(5) | Ca |
| Ca3 | 0.0081(6) | 0.0280(8) | 0.0115(7) | 0.0003(6) | -0.0002(6) | -0.0044(6) | Ca |
| Nb11 | 0.0032(3) | 0.0041(3) | 0.0042(3) | 0.0001(2) | -0.00012(14) | 0.00052(14) | Nb |
| Ti11 | 0.0032(3) | 0.0041(3) | 0.0042(3) | 0.0001(2) | -0.00012(14) | 0.00052(14) | Ti |
| Nb12 | 0.0032(3) | 0.0041(3) | 0.0042(3) | 0.0001(2) | -0.00012(14) | 0.00052(14) | Nb |
| Ti12 | 0.0032(3) | 0.0041(3) | 0.0042(3) | 0.0001(2) | -0.00012(14) | 0.00052(14) | Ti |
| Nb13 | 0.0032(3) | 0.0041(3) | 0.0042(3) | 0.0001(2) | -0.00012(14) | 0.00052(14) | Nb |
| Ti13 | 0.0032(3) | 0.0041(3) | 0.0042(3) | 0.0001(2) | -0.00012(14) | 0.00052(14) | Ti |
| Nb21 | 0.0032(3) | 0.0043(3) | 0.0042(3) | -0.0005(2) | 0.00000(14) | 0.00025(13) | Nb |
| Ti21 | 0.0032(3) | 0.0043(3) | 0.0042(3) | -0.0005(2) | 0.00000(14) | 0.00025(13) | Ti |
| Nb22 | 0.0032(3) | 0.0043(3) | 0.0042(3) | -0.0005(2) | 0.00000(14) | 0.00025(13) | Nb |
| Ti22 | 0.0032(3) | 0.0043(3) | 0.0042(3) | -0.0005(2) | 0.00000(14) | 0.00025(13) | Ti |
| Nb23 | 0.0032(3) | 0.0043(3) | 0.0042(3) | -0.0005(2) | 0.00000(14) | 0.00025(13) | Nb |
| Ti23 | 0.0032(3) | 0.0043(3) | 0.0042(3) | -0.0005(2) | 0.00000(14) | 0.00025(13) | Ti |
| O1 | 0.0046(10) | 0.0096(11) | 0.0065(10) | 0.0000(8) | 0.0003(7) | 0.0010(7) | O |
| O2 | 0.0077(9) | 0.0072(9) | 0.0070(8) | -0.0006(7) | -0.0011(7) | 0.0021(7) | O |
| O3 | 0.0088(9) | 0.0062(9) | 0.0081(9) | 0.0002(7) | 0.0008(7) | 0.0020(7) | O |
Fourier Wave Vectors (explicit: q_x,q_y,q_z or coefficients: q_1,q_2,...): (Show/hide table) [ Help ]
| Wave vector code | q_x | q_y | q_z |
|---|---|---|---|
| 1 | 0.00000 | 0.08333 | 0.00000 |
| 2 | 0.00000 | 0.16666 | 0.00000 |
| 3 | 0.00000 | 0.24999 | 0.00000 |
| 4 | 0.00000 | 0.33332 | 0.00000 |
| 5 | 0.00000 | 0.41665 | 0.00000 |
| 6 | 0.00000 | 0.49998 | 0.00000 |
Definition of the displacive (translational) Fourier series: (Show/hide table) [ Help ]
| Modulation code | Atom site label | Displacement axis | Wave vector code |
|---|---|---|---|
| Ca1x1 | Ca1 | x | 1 |
| Ca1y1 | Ca1 | y | 1 |
| Ca1z1 | Ca1 | z | 1 |
| Nb11x1 | Nb11 | x | 1 |
| Nb11y1 | Nb11 | y | 1 |
| Nb11z1 | Nb11 | z | 1 |
| Nb11x2 | Nb11 | x | 2 |
| Nb11y2 | Nb11 | y | 2 |
| Nb11z2 | Nb11 | z | 2 |
| Nb11x3 | Nb11 | x | 3 |
| Nb11y3 | Nb11 | y | 3 |
| Nb11z3 | Nb11 | z | 3 |
| Nb11x4 | Nb11 | x | 4 |
| Nb11y4 | Nb11 | y | 4 |
| Nb11z4 | Nb11 | z | 4 |
| Nb11x5 | Nb11 | x | 5 |
| Nb11y5 | Nb11 | y | 5 |
| Nb11z5 | Nb11 | z | 5 |
| Nb11x6 | Nb11 | x | 6 |
| Nb11y6 | Nb11 | y | 6 |
| Nb11z6 | Nb11 | z | 6 |
| Ti11x1 | Ti11 | x | 1 |
| Ti11y1 | Ti11 | y | 1 |
| Ti11z1 | Ti11 | z | 1 |
| Ti11x2 | Ti11 | x | 2 |
| Ti11y2 | Ti11 | y | 2 |
| Ti11z2 | Ti11 | z | 2 |
| Ti11x3 | Ti11 | x | 3 |
| Ti11y3 | Ti11 | y | 3 |
| Ti11z3 | Ti11 | z | 3 |
| Ti11x4 | Ti11 | x | 4 |
| Ti11y4 | Ti11 | y | 4 |
| Ti11z4 | Ti11 | z | 4 |
| Ti11x5 | Ti11 | x | 5 |
| Ti11y5 | Ti11 | y | 5 |
| Ti11z5 | Ti11 | z | 5 |
| Ti11x6 | Ti11 | x | 6 |
| Ti11y6 | Ti11 | y | 6 |
| Ti11z6 | Ti11 | z | 6 |
| Nb12x1 | Nb12 | x | 1 |
| Nb12y1 | Nb12 | y | 1 |
| Nb12z1 | Nb12 | z | 1 |
| Nb12x2 | Nb12 | x | 2 |
| Nb12y2 | Nb12 | y | 2 |
| Nb12z2 | Nb12 | z | 2 |
| Nb12x3 | Nb12 | x | 3 |
| Nb12y3 | Nb12 | y | 3 |
| Nb12z3 | Nb12 | z | 3 |
| Nb12x4 | Nb12 | x | 4 |
| Nb12y4 | Nb12 | y | 4 |
| Nb12z4 | Nb12 | z | 4 |
| Nb12x5 | Nb12 | x | 5 |
| Nb12y5 | Nb12 | y | 5 |
| Nb12z5 | Nb12 | z | 5 |
| Nb12x6 | Nb12 | x | 6 |
| Nb12y6 | Nb12 | y | 6 |
| Nb12z6 | Nb12 | z | 6 |
| Ti12x1 | Ti12 | x | 1 |
| Ti12y1 | Ti12 | y | 1 |
| Ti12z1 | Ti12 | z | 1 |
| Ti12x2 | Ti12 | x | 2 |
| Ti12y2 | Ti12 | y | 2 |
| Ti12z2 | Ti12 | z | 2 |
| Ti12x3 | Ti12 | x | 3 |
| Ti12y3 | Ti12 | y | 3 |
| Ti12z3 | Ti12 | z | 3 |
| Ti12x4 | Ti12 | x | 4 |
| Ti12y4 | Ti12 | y | 4 |
| Ti12z4 | Ti12 | z | 4 |
| Ti12x5 | Ti12 | x | 5 |
| Ti12y5 | Ti12 | y | 5 |
| Ti12z5 | Ti12 | z | 5 |
| Ti12x6 | Ti12 | x | 6 |
| Ti12y6 | Ti12 | y | 6 |
| Ti12z6 | Ti12 | z | 6 |
| Nb13x1 | Nb13 | x | 1 |
| Nb13y1 | Nb13 | y | 1 |
| Nb13z1 | Nb13 | z | 1 |
| Nb13x2 | Nb13 | x | 2 |
| Nb13y2 | Nb13 | y | 2 |
| Nb13z2 | Nb13 | z | 2 |
| Nb13x3 | Nb13 | x | 3 |
| Nb13y3 | Nb13 | y | 3 |
| Nb13z3 | Nb13 | z | 3 |
| Nb13x4 | Nb13 | x | 4 |
| Nb13y4 | Nb13 | y | 4 |
| Nb13z4 | Nb13 | z | 4 |
| Nb13x5 | Nb13 | x | 5 |
| Nb13y5 | Nb13 | y | 5 |
| Nb13z5 | Nb13 | z | 5 |
| Nb13x6 | Nb13 | x | 6 |
| Nb13y6 | Nb13 | y | 6 |
| Nb13z6 | Nb13 | z | 6 |
| Ti13x1 | Ti13 | x | 1 |
| Ti13y1 | Ti13 | y | 1 |
| Ti13z1 | Ti13 | z | 1 |
| Ti13x2 | Ti13 | x | 2 |
| Ti13y2 | Ti13 | y | 2 |
| Ti13z2 | Ti13 | z | 2 |
| Ti13x3 | Ti13 | x | 3 |
| Ti13y3 | Ti13 | y | 3 |
| Ti13z3 | Ti13 | z | 3 |
| Ti13x4 | Ti13 | x | 4 |
| Ti13y4 | Ti13 | y | 4 |
| Ti13z4 | Ti13 | z | 4 |
| Ti13x5 | Ti13 | x | 5 |
| Ti13y5 | Ti13 | y | 5 |
| Ti13z5 | Ti13 | z | 5 |
| Ti13x6 | Ti13 | x | 6 |
| Ti13y6 | Ti13 | y | 6 |
| Ti13z6 | Ti13 | z | 6 |
| Nb21x1 | Nb21 | x | 1 |
| Nb21y1 | Nb21 | y | 1 |
| Nb21z1 | Nb21 | z | 1 |
| Nb21x2 | Nb21 | x | 2 |
| Nb21y2 | Nb21 | y | 2 |
| Nb21z2 | Nb21 | z | 2 |
| Nb21x3 | Nb21 | x | 3 |
| Nb21y3 | Nb21 | y | 3 |
| Nb21z3 | Nb21 | z | 3 |
| Nb21x4 | Nb21 | x | 4 |
| Nb21y4 | Nb21 | y | 4 |
| Nb21z4 | Nb21 | z | 4 |
| Nb21x5 | Nb21 | x | 5 |
| Nb21y5 | Nb21 | y | 5 |
| Nb21z5 | Nb21 | z | 5 |
| Nb21x6 | Nb21 | x | 6 |
| Nb21y6 | Nb21 | y | 6 |
| Nb21z6 | Nb21 | z | 6 |
| Ti21x1 | Ti21 | x | 1 |
| Ti21y1 | Ti21 | y | 1 |
| Ti21z1 | Ti21 | z | 1 |
| Ti21x2 | Ti21 | x | 2 |
| Ti21y2 | Ti21 | y | 2 |
| Ti21z2 | Ti21 | z | 2 |
| Ti21x3 | Ti21 | x | 3 |
| Ti21y3 | Ti21 | y | 3 |
| Ti21z3 | Ti21 | z | 3 |
| Ti21x4 | Ti21 | x | 4 |
| Ti21y4 | Ti21 | y | 4 |
| Ti21z4 | Ti21 | z | 4 |
| Ti21x5 | Ti21 | x | 5 |
| Ti21y5 | Ti21 | y | 5 |
| Ti21z5 | Ti21 | z | 5 |
| Ti21x6 | Ti21 | x | 6 |
| Ti21y6 | Ti21 | y | 6 |
| Ti21z6 | Ti21 | z | 6 |
| Nb22x1 | Nb22 | x | 1 |
| Nb22y1 | Nb22 | y | 1 |
| Nb22z1 | Nb22 | z | 1 |
| Nb22x2 | Nb22 | x | 2 |
| Nb22y2 | Nb22 | y | 2 |
| Nb22z2 | Nb22 | z | 2 |
| Nb22x3 | Nb22 | x | 3 |
| Nb22y3 | Nb22 | y | 3 |
| Nb22z3 | Nb22 | z | 3 |
| Nb22x4 | Nb22 | x | 4 |
| Nb22y4 | Nb22 | y | 4 |
| Nb22z4 | Nb22 | z | 4 |
| Nb22x5 | Nb22 | x | 5 |
| Nb22y5 | Nb22 | y | 5 |
| Nb22z5 | Nb22 | z | 5 |
| Nb22x6 | Nb22 | x | 6 |
| Nb22y6 | Nb22 | y | 6 |
| Nb22z6 | Nb22 | z | 6 |
| Ti22x1 | Ti22 | x | 1 |
| Ti22y1 | Ti22 | y | 1 |
| Ti22z1 | Ti22 | z | 1 |
| Ti22x2 | Ti22 | x | 2 |
| Ti22y2 | Ti22 | y | 2 |
| Ti22z2 | Ti22 | z | 2 |
| Ti22x3 | Ti22 | x | 3 |
| Ti22y3 | Ti22 | y | 3 |
| Ti22z3 | Ti22 | z | 3 |
| Ti22x4 | Ti22 | x | 4 |
| Ti22y4 | Ti22 | y | 4 |
| Ti22z4 | Ti22 | z | 4 |
| Ti22x5 | Ti22 | x | 5 |
| Ti22y5 | Ti22 | y | 5 |
| Ti22z5 | Ti22 | z | 5 |
| Ti22x6 | Ti22 | x | 6 |
| Ti22y6 | Ti22 | y | 6 |
| Ti22z6 | Ti22 | z | 6 |
| Nb23x1 | Nb23 | x | 1 |
| Nb23y1 | Nb23 | y | 1 |
| Nb23z1 | Nb23 | z | 1 |
| Nb23x2 | Nb23 | x | 2 |
| Nb23y2 | Nb23 | y | 2 |
| Nb23z2 | Nb23 | z | 2 |
| Nb23x3 | Nb23 | x | 3 |
| Nb23y3 | Nb23 | y | 3 |
| Nb23z3 | Nb23 | z | 3 |
| Nb23x4 | Nb23 | x | 4 |
| Nb23y4 | Nb23 | y | 4 |
| Nb23z4 | Nb23 | z | 4 |
| Nb23x5 | Nb23 | x | 5 |
| Nb23y5 | Nb23 | y | 5 |
| Nb23z5 | Nb23 | z | 5 |
| Nb23x6 | Nb23 | x | 6 |
| Nb23y6 | Nb23 | y | 6 |
| Nb23z6 | Nb23 | z | 6 |
| Ti23x1 | Ti23 | x | 1 |
| Ti23y1 | Ti23 | y | 1 |
| Ti23z1 | Ti23 | z | 1 |
| Ti23x2 | Ti23 | x | 2 |
| Ti23y2 | Ti23 | y | 2 |
| Ti23z2 | Ti23 | z | 2 |
| Ti23x3 | Ti23 | x | 3 |
| Ti23y3 | Ti23 | y | 3 |
| Ti23z3 | Ti23 | z | 3 |
| Ti23x4 | Ti23 | x | 4 |
| Ti23y4 | Ti23 | y | 4 |
| Ti23z4 | Ti23 | z | 4 |
| Ti23x5 | Ti23 | x | 5 |
| Ti23y5 | Ti23 | y | 5 |
| Ti23z5 | Ti23 | z | 5 |
| Ti23x6 | Ti23 | x | 6 |
| Ti23y6 | Ti23 | y | 6 |
| Ti23z6 | Ti23 | z | 6 |
| O1x1 | O1 | x | 1 |
| O1y1 | O1 | y | 1 |
| O1z1 | O1 | z | 1 |
| O1x2 | O1 | x | 2 |
| O1y2 | O1 | y | 2 |
| O1z2 | O1 | z | 2 |
| O2x1 | O2 | x | 1 |
| O2y1 | O2 | y | 1 |
| O2z1 | O2 | z | 1 |
| O2x2 | O2 | x | 2 |
| O2y2 | O2 | y | 2 |
| O2z2 | O2 | z | 2 |
| O2x3 | O2 | x | 3 |
| O2y3 | O2 | y | 3 |
| O2z3 | O2 | z | 3 |
| O3x1 | O3 | x | 1 |
| O3y1 | O3 | y | 1 |
| O3z1 | O3 | z | 1 |
| O3x2 | O3 | x | 2 |
| O3y2 | O3 | y | 2 |
| O3z2 | O3 | z | 2 |
| O3x3 | O3 | x | 3 |
| O3y3 | O3 | y | 3 |
| O3z3 | O3 | z | 3 |
Displacive (translational) Fourier coefficients: (Show/hide table) [ Help ]
| Modulation code | Cosine coefficient | Sine coefficient |
|---|---|---|
| Ca1x1 | -0.00027(12) | 0.00099(12) |
| Ca1y1 | 0.00212(16) | 0.02237(16) |
| Ca1z1 | 0.0009(2) | 0.00112(15) |
| Nb11x1 | 0 | -0.00370(14) |
| Nb11y1 | 0 | 0.1230(2) |
| Nb11z1 | 0 | -0.0441(2) |
| Nb11x2 | 0 | 0 |
| Nb11y2 | 0 | 0 |
| Nb11z2 | 0 | 0 |
| Nb11x3 | 0 | 0 |
| Nb11y3 | 0 | 0 |
| Nb11z3 | 0 | 0 |
| Nb11x4 | 0 | 0 |
| Nb11y4 | 0 | 0 |
| Nb11z4 | 0 | 0 |
| Nb11x5 | 0 | 0 |
| Nb11y5 | 0 | 0 |
| Nb11z5 | 0 | 0 |
| Nb11x6 | 0 | 0.00245(8) |
| Nb11y6 | 0 | 0.01122(11) |
| Nb11z6 | 0 | 0.01475(13) |
| Ti11x1 | 0 | -0.00370(14) |
| Ti11y1 | 0 | 0.1230(2) |
| Ti11z1 | 0 | -0.0441(2) |
| Ti11x2 | 0 | 0 |
| Ti11y2 | 0 | 0 |
| Ti11z2 | 0 | 0 |
| Ti11x3 | 0 | 0 |
| Ti11y3 | 0 | 0 |
| Ti11z3 | 0 | 0 |
| Ti11x4 | 0 | 0 |
| Ti11y4 | 0 | 0 |
| Ti11z4 | 0 | 0 |
| Ti11x5 | 0 | 0 |
| Ti11y5 | 0 | 0 |
| Ti11z5 | 0 | 0 |
| Ti11x6 | 0 | 0.00245(8) |
| Ti11y6 | 0 | 0.01122(11) |
| Ti11z6 | 0 | 0.01475(13) |
| Nb12x1 | 0 | -0.00369(14) |
| Nb12y1 | 0 | 0.1230(2) |
| Nb12z1 | 0 | -0.0441(2) |
| Nb12x2 | 0 | 0 |
| Nb12y2 | 0 | 0 |
| Nb12z2 | 0 | 0 |
| Nb12x3 | 0 | 0 |
| Nb12y3 | 0 | 0 |
| Nb12z3 | 0 | 0 |
| Nb12x4 | 0 | 0 |
| Nb12y4 | 0 | 0 |
| Nb12z4 | 0 | 0 |
| Nb12x5 | 0 | 0 |
| Nb12y5 | 0 | 0 |
| Nb12z5 | 0 | 0 |
| Nb12x6 | 0 | 0.00245(8) |
| Nb12y6 | 0 | 0.01122(11) |
| Nb12z6 | 0 | 0.01475(13) |
| Ti12x1 | 0 | -0.00369(14) |
| Ti12y1 | 0 | 0.1230(2) |
| Ti12z1 | 0 | -0.0441(2) |
| Ti12x2 | 0 | 0 |
| Ti12y2 | 0 | 0 |
| Ti12z2 | 0 | 0 |
| Ti12x3 | 0 | 0 |
| Ti12y3 | 0 | 0 |
| Ti12z3 | 0 | 0 |
| Ti12x4 | 0 | 0 |
| Ti12y4 | 0 | 0 |
| Ti12z4 | 0 | 0 |
| Ti12x5 | 0 | 0 |
| Ti12y5 | 0 | 0 |
| Ti12z5 | 0 | 0 |
| Ti12x6 | 0 | 0.00245(8) |
| Ti12y6 | 0 | 0.01122(11) |
| Ti12z6 | 0 | 0.01475(13) |
| Nb13x1 | 0 | -0.00369(14) |
| Nb13y1 | 0 | 0.1230(2) |
| Nb13z1 | 0 | -0.0441(2) |
| Nb13x2 | 0 | 0 |
| Nb13y2 | 0 | 0 |
| Nb13z2 | 0 | 0 |
| Nb13x3 | 0 | 0 |
| Nb13y3 | 0 | 0 |
| Nb13z3 | 0 | 0 |
| Nb13x4 | 0 | 0 |
| Nb13y4 | 0 | 0 |
| Nb13z4 | 0 | 0 |
| Nb13x5 | 0 | 0 |
| Nb13y5 | 0 | 0 |
| Nb13z5 | 0 | 0 |
| Nb13x6 | 0 | 0.00245(8) |
| Nb13y6 | 0 | 0.01122(11) |
| Nb13z6 | 0 | 0.01475(13) |
| Ti13x1 | 0 | -0.00369(14) |
| Ti13y1 | 0 | 0.1230(2) |
| Ti13z1 | 0 | -0.0441(2) |
| Ti13x2 | 0 | 0 |
| Ti13y2 | 0 | 0 |
| Ti13z2 | 0 | 0 |
| Ti13x3 | 0 | 0 |
| Ti13y3 | 0 | 0 |
| Ti13z3 | 0 | 0 |
| Ti13x4 | 0 | 0 |
| Ti13y4 | 0 | 0 |
| Ti13z4 | 0 | 0 |
| Ti13x5 | 0 | 0 |
| Ti13y5 | 0 | 0 |
| Ti13z5 | 0 | 0 |
| Ti13x6 | 0 | 0.00245(8) |
| Ti13y6 | 0 | 0.01122(11) |
| Ti13z6 | 0 | 0.01475(13) |
| Nb21x1 | 0 | 0.01104(14) |
| Nb21y1 | 0 | 0.1349(2) |
| Nb21z1 | 0 | -0.0506(2) |
| Nb21x2 | 0 | 0 |
| Nb21y2 | 0 | 0 |
| Nb21z2 | 0 | 0 |
| Nb21x3 | 0 | 0 |
| Nb21y3 | 0 | 0 |
| Nb21z3 | 0 | 0 |
| Nb21x4 | 0 | 0 |
| Nb21y4 | 0 | 0 |
| Nb21z4 | 0 | 0 |
| Nb21x5 | 0 | 0 |
| Nb21y5 | 0 | 0 |
| Nb21z5 | 0 | 0 |
| Nb21x6 | 0 | -0.00387(8) |
| Nb21y6 | 0 | 0.01223(11) |
| Nb21z6 | 0 | 0.01510(13) |
| Ti21x1 | 0 | 0.01104(14) |
| Ti21y1 | 0 | 0.1349(2) |
| Ti21z1 | 0 | -0.0506(2) |
| Ti21x2 | 0 | 0 |
| Ti21y2 | 0 | 0 |
| Ti21z2 | 0 | 0 |
| Ti21x3 | 0 | 0 |
| Ti21y3 | 0 | 0 |
| Ti21z3 | 0 | 0 |
| Ti21x4 | 0 | 0 |
| Ti21y4 | 0 | 0 |
| Ti21z4 | 0 | 0 |
| Ti21x5 | 0 | 0 |
| Ti21y5 | 0 | 0 |
| Ti21z5 | 0 | 0 |
| Ti21x6 | 0 | -0.00387(8) |
| Ti21y6 | 0 | 0.01223(11) |
| Ti21z6 | 0 | 0.01510(13) |
| Nb22x1 | 0 | 0.01104(14) |
| Nb22y1 | 0 | 0.1349(2) |
| Nb22z1 | 0 | -0.0506(2) |
| Nb22x2 | 0 | 0 |
| Nb22y2 | 0 | 0 |
| Nb22z2 | 0 | 0 |
| Nb22x3 | 0 | 0 |
| Nb22y3 | 0 | 0 |
| Nb22z3 | 0 | 0 |
| Nb22x4 | 0 | 0 |
| Nb22y4 | 0 | 0 |
| Nb22z4 | 0 | 0 |
| Nb22x5 | 0 | 0 |
| Nb22y5 | 0 | 0 |
| Nb22z5 | 0 | 0 |
| Nb22x6 | 0 | -0.00387(8) |
| Nb22y6 | 0 | 0.01223(11) |
| Nb22z6 | 0 | 0.01510(13) |
| Ti22x1 | 0 | 0.01104(14) |
| Ti22y1 | 0 | 0.1349(2) |
| Ti22z1 | 0 | -0.0506(2) |
| Ti22x2 | 0 | 0 |
| Ti22y2 | 0 | 0 |
| Ti22z2 | 0 | 0 |
| Ti22x3 | 0 | 0 |
| Ti22y3 | 0 | 0 |
| Ti22z3 | 0 | 0 |
| Ti22x4 | 0 | 0 |
| Ti22y4 | 0 | 0 |
| Ti22z4 | 0 | 0 |
| Ti22x5 | 0 | 0 |
| Ti22y5 | 0 | 0 |
| Ti22z5 | 0 | 0 |
| Ti22x6 | 0 | -0.00387(8) |
| Ti22y6 | 0 | 0.01223(11) |
| Ti22z6 | 0 | 0.01510(13) |
| Nb23x1 | 0 | 0.01104(14) |
| Nb23y1 | 0 | 0.1349(2) |
| Nb23z1 | 0 | -0.0506(2) |
| Nb23x2 | 0 | 0 |
| Nb23y2 | 0 | 0 |
| Nb23z2 | 0 | 0 |
| Nb23x3 | 0 | 0 |
| Nb23y3 | 0 | 0 |
| Nb23z3 | 0 | 0 |
| Nb23x4 | 0 | 0 |
| Nb23y4 | 0 | 0 |
| Nb23z4 | 0 | 0 |
| Nb23x5 | 0 | 0 |
| Nb23y5 | 0 | 0 |
| Nb23z5 | 0 | 0 |
| Nb23x6 | 0 | -0.00387(8) |
| Nb23y6 | 0 | 0.01223(11) |
| Nb23z6 | 0 | 0.01510(13) |
| Ti23x1 | 0 | 0.01104(14) |
| Ti23y1 | 0 | 0.1349(2) |
| Ti23z1 | 0 | -0.0506(2) |
| Ti23x2 | 0 | 0 |
| Ti23y2 | 0 | 0 |
| Ti23z2 | 0 | 0 |
| Ti23x3 | 0 | 0 |
| Ti23y3 | 0 | 0 |
| Ti23z3 | 0 | 0 |
| Ti23x4 | 0 | 0 |
| Ti23y4 | 0 | 0 |
| Ti23z4 | 0 | 0 |
| Ti23x5 | 0 | 0 |
| Ti23y5 | 0 | 0 |
| Ti23z5 | 0 | 0 |
| Ti23x6 | 0 | -0.00387(8) |
| Ti23y6 | 0 | 0.01223(11) |
| Ti23z6 | 0 | 0.01510(13) |
| O1x1 | -0.0001(3) | 0.0003(3) |
| O1y1 | 0.0116(4) | 0.0052(4) |
| O1z1 | -0.0037(4) | -0.0052(3) |
| O1x2 | 0.0004(4) | -0.0006(3) |
| O1y2 | -0.0028(5) | -0.0078(4) |
| O1z2 | 0.0025(6) | 0.0020(4) |
| O2x1 | -0.0070(2) | 0.0029(2) |
| O2y1 | -0.0099(3) | 0.0229(3) |
| O2z1 | 0.0021(3) | 0.0023(4) |
| O2x2 | 0.0029(3) | 0.0084(3) |
| O2y2 | 0.0051(4) | -0.0103(4) |
| O2z2 | 0.0008(4) | -0.0060(5) |
| O2x3 | 0 | -0.0045(4) |
| O2y3 | 0 | 0.0033(5) |
| O2z3 | 0 | 0.0048(6) |
| O3x1 | 0.0037(3) | 0.0001(2) |
| O3y1 | 0.0037(4) | 0.0188(4) |
| O3z1 | 0.0094(4) | 0.0001(4) |
| O3x2 | -0.0019(3) | -0.0107(3) |
| O3y2 | 0.0019(4) | -0.0077(4) |
| O3z2 | 0.0000(5) | -0.0058(5) |
| O3x3 | 0 | 0.0055(4) |
| O3y3 | 0 | 0.0029(5) |
| O3z3 | 0 | 0.0043(6) |
Definition of the ADP Fourier series: (Show/hide table) [ Help ]
| Modulation code | Atom site label | Tensor element | Wave vector code |
|---|---|---|---|
| Ca1U111 | Ca1 | U11 | 1 |
| Ca1U221 | Ca1 | U22 | 1 |
| Ca1U331 | Ca1 | U33 | 1 |
| Ca1U121 | Ca1 | U12 | 1 |
| Ca1U131 | Ca1 | U13 | 1 |
| Ca1U231 | Ca1 | U23 | 1 |
ADP Fourier coefficients: (Show/hide table) [ Help ]
| Modulation code | Cosine coefficient | Sine coefficient |
|---|---|---|
| Ca1U111 | -0.0001(4) | 0.0025(3) |
| Ca1U221 | -0.0022(5) | 0.0042(4) |
| Ca1U331 | -0.0011(5) | 0.0032(4) |
| Ca1U121 | -0.0004(4) | 0.0000(3) |
| Ca1U131 | 0.0004(5) | -0.0003(4) |
| Ca1U231 | 0.0013(5) | -0.0015(3) |
Occupation crenel coefficients: (Show/hide table) [ Help ]
| Atom site label | Center (x0) | Width |
|---|---|---|
| Ca1 | 0 | 0.125 |
| Ca2 | 0.11083(2) | 0.0417 |
| Ca3 | -0.10416(2) | 0.0417 |
| Nb11 | 0 | 0.0417 |
| Ti11 | 0 | 0.0417 |
| Nb12 | 0.0417 | 0.0417 |
| Ti12 | 0.0417 | 0.0417 |
| Nb13 | 0.0833 | 0.0417 |
| Ti13 | 0.0833 | 0.0417 |
| Nb21 | 0 | 0.0417 |
| Ti21 | 0 | 0.0417 |
| Nb22 | 0.0417 | 0.0417 |
| Ti22 | 0.0417 | 0.0417 |
| Nb23 | 0.0833 | 0.0417 |
| Ti23 | 0.0833 | 0.0417 |
| O1 | 0 | 0.2083 |
| O2 | 0 | 0.25 |
| O3 | 0 | 0.25 |
Ca6_Nb_6_Ti6_O20
Chemical data
Structural Formula Sum: Ca3.429 Nb2.606 O11.429 Ti0.823 [ Help ]
Formula weight: 601.8 Da [ Help ]
Crystallographic data and experimental details
Crystal system: monoclinic [ Help ]
Superspace group name: C'21/d(σ1σ20)-10 [ Help ]
Symmetry operations of the superspace group: (Show/hide table) [ Help ]
| Operation code | Operation in algebraic form |
|---|---|
| 1 | x1,x2,x3,x4 |
| 2 | -x1,-x2,-x3,1/2-x4 |
| 3 | 1/4-x1,-x2,1/2+x3,1/4-x4 |
| 4 | x1,1/2+x2,1/2-x3,x4 |
| 5 | 3/4+x1,1/2+x2,x3,1/4+x4 |
| 6 | 3/4-x1,1/2-x2,-x3,3/4-x4 |
| 7 | -x1,1/2-x2,1/2+x3,1/2-x4 |
| 8 | 3/4+x1,x2,1/2-x3,1/4+x4 |
| 9 | 1/2+x1,x2,x3,1/2+x4 |
| 10 | 1/2-x1,-x2,-x3,-x4 |
| 11 | 3/4-x1,-x2,1/2+x3,3/4-x4 |
| 12 | 1/2+x1,1/2+x2,1/2-x3,1/2+x4 |
| 13 | 1/4+x1,1/2+x2,x3,3/4+x4 |
| 14 | 1/4-x1,1/2-x2,-x3,1/4-x4 |
| 15 | 1/2-x1,1/2-x2,1/2+x3,-x4 |
| 16 | 1/4+x1,x2,1/2-x3,3/4+x4 |
a: 7.6805(3) Å [ Help ]
b: 5.3641(3) Å [ Help ]
c: 5.46530(10) Å [ Help ]
α: 90 ° [ Help ]
β: 90 ° [ Help ]
γ: 90.036(4) ° [ Help ]
Volume: 225.165(16) Å3 [ Help ]
Z: 1 [ Help ]
Modulation dimension: 1 [ Help ]
Measured independent wave vectors: (Show/hide table) [ Help ]
| Wave vector id | q_x | q_y | q_z |
|---|---|---|---|
| 1 | 0.00000 | 0.07143 | 0.00000 |
μ: 5.773 mm-1 [ Help ]
Absorption correction type: none [ Help ]
Minimum transmission factor: 1.000 [ Help ]
Maximum transmission factor: 1.000 [ Help ]
Refinement details
Total nb. of reflections: 5863 [ Help ]
Nb. of observed reflections: 5186 [ Help ]
Intense reflections threshold: I>3σ(I) [ Help ]
Refinement based on: F [ Help ]
R(all): 0.0647 [ Help ]
R(obs): 0.0581 [ Help ]
wR(obs): 0.0652 [ Help ]
wR(all): 0.0666 [ Help ]
S(all): 2.59 [ Help ]
Nb. of reflections: 5863 [ Help ]
Nb. of parameters: 162 [ Help ]
Weighting scheme: sigma [ Help ]
Weighting scheme remarks: w=1/(σ2(F)+0.0001F2) [ Help ]
Δ/σ(max): 0.0064 [ Help ]
Δ/σ(mean): 0.0003 [ Help ]
Δρ(max): 1.62 e_Å-3 [ Help ]
Δρ(min): -1.31 e_Å-3 [ Help ]
Extinction method: B-C type 1 Gaussian isotropic (Becker & Coppens, 1974) [ Help ]
Extinction coefficient: 0.053181 [ Help ]
Structural Information
Average Structure: (Show/hide table) [ Help ]
| Atom symbol | Atom site label | x | y | z | Uiso/equiv | ADP type | Coords from (d)iffraction or (c)alculated | Coords restraints or constraints | Occupancy | Disordered cluster | Disordered group |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ca | Ca1 | -0.00001(9) | -0.03449(14) | 0.00458(12) | 0.0128(2) | Uani | d | . | 0.1429 | . | . |
| Ca | Ca2 | 0.0016(2) | 0.3320(2) | -0.0872(3) | 0.0070(3) | Uani | d | . | 0.0357 | . | . |
| Ca | Ca3 | -0.0085(2) | -0.2496(3) | 0.0171(4) | 0.0134(4) | Uani | d | . | 0.0357 | . | . |
| Nb | Nb11 | 0.25 | 0 | 0.5 | 0.00746(13) | Uani | d | . | 0.032(6) | . | . |
| Ti | Ti11 | 0.25 | 0 | 0.5 | 0.00746(13) | Uani | d | . | 0.040(6) | . | . |
| Nb | Nb12 | 0.25 | 0 | 0.5 | 0.00746(13) | Uani | d | . | 0.127(14) | . | . |
| Ti | Ti12 | 0.25 | 0 | 0.5 | 0.00746(13) | Uani | d | . | 0.016(14) | . | . |
| Nb | Nb13 | 0.25 | 0 | 0.5 | 0.00746(13) | Uani | d | . | 0.071(6) | . | . |
| Ti | Ti13 | 0.25 | 0 | 0.5 | 0.00746(13) | Uani | d | . | 0.001(6) | . | . |
| Nb | Nb21 | 0.75 | 0 | 0.5 | 0.00710(13) | Uani | d | . | 0.034(6) | . | . |
| Ti | Ti21 | 0.75 | 0 | 0.5 | 0.00710(13) | Uani | d | . | 0.038(6) | . | . |
| Nb | Nb22 | 0.75 | 0 | 0.5 | 0.00710(13) | Uani | d | . | 0.129(14) | . | . |
| Ti | Ti22 | 0.75 | 0 | 0.5 | 0.00710(13) | Uani | d | . | 0.013(14) | . | . |
| Nb | Nb23 | 0.75 | 0 | 0.5 | 0.00710(13) | Uani | d | . | 0.071(14) | . | . |
| Ti | Ti23 | 0.75 | 0 | 0.5 | 0.00710(13) | Uani | d | . | 0.000(14) | . | . |
| O | O1 | -0.0002(2) | 0.0147(3) | 0.5799(4) | 0.0093(5) | Uani | d | . | 0.2143 | . | . |
| O | O2 | 0.2140(2) | 0.2112(3) | 0.2056(3) | 0.0080(5) | Uani | d | . | 0.25 | . | . |
| O | O3 | 0.7869(2) | 0.1981(3) | 0.1964(3) | 0.0100(5) | Uani | d | . | 0.25 | . | . |
ADP components: (Show/hide table) [ Help ]
| Atom site label | U11 | U22 | U33 | U12 | U13 | U23 | Atom site symbol |
|---|---|---|---|---|---|---|---|
| Ca1 | 0.0107(4) | 0.0144(3) | 0.0133(4) | -0.0005(3) | 0.0003(4) | -0.0028(3) | Ca |
| Ca2 | 0.0067(6) | 0.0084(6) | 0.0060(6) | -0.0021(6) | 0.0003(7) | 0.0017(5) | Ca |
| Ca3 | 0.0078(6) | 0.0250(7) | 0.0074(6) | 0.0027(7) | -0.0023(8) | -0.0001(7) | Ca |
| Nb11 | 0.0058(2) | 0.0081(2) | 0.0086(2) | -0.0037(3) | -0.0001(3) | 0.00002(15) | Nb |
| Ti11 | 0.0058(2) | 0.0081(2) | 0.0086(2) | -0.0037(3) | -0.0001(3) | 0.00002(15) | Ti |
| Nb12 | 0.0058(2) | 0.0081(2) | 0.0086(2) | -0.0037(3) | -0.0001(3) | 0.00002(15) | Nb |
| Ti12 | 0.0058(2) | 0.0081(2) | 0.0086(2) | -0.0037(3) | -0.0001(3) | 0.00002(15) | Ti |
| Nb13 | 0.0058(2) | 0.0081(2) | 0.0086(2) | -0.0037(3) | -0.0001(3) | 0.00003(15) | Nb |
| Ti13 | 0.0058(2) | 0.0081(2) | 0.0086(2) | -0.0037(3) | -0.0001(3) | 0.00003(15) | Ti |
| Nb21 | 0.0053(2) | 0.0080(2) | 0.0080(2) | -0.0041(3) | -0.0006(2) | 0.00040(15) | Nb |
| Ti21 | 0.0053(2) | 0.0080(2) | 0.0080(2) | -0.0041(3) | -0.0006(2) | 0.00040(15) | Ti |
| Nb22 | 0.0053(2) | 0.0080(2) | 0.0080(2) | -0.0041(3) | -0.0006(2) | 0.00040(15) | Nb |
| Ti22 | 0.0053(2) | 0.0080(2) | 0.0080(2) | -0.0041(3) | -0.0006(2) | 0.00040(15) | Ti |
| Nb23 | 0.0053(2) | 0.0080(2) | 0.0080(2) | -0.0041(3) | -0.0006(2) | 0.00040(15) | Nb |
| Ti23 | 0.0053(2) | 0.0080(2) | 0.0080(2) | -0.0041(3) | -0.0006(2) | 0.00040(15) | Ti |
| O1 | 0.0040(9) | 0.0117(9) | 0.0121(10) | -0.0020(8) | -0.0001(7) | 0.0002(6) | O |
| O2 | 0.0040(10) | 0.0094(8) | 0.0106(8) | -0.0019(7) | -0.0025(7) | 0.0001(6) | O |
| O3 | 0.0099(11) | 0.0099(8) | 0.0101(8) | -0.0010(7) | -0.0002(7) | 0.0027(6) | O |
Fourier Wave Vectors (explicit: q_x,q_y,q_z or coefficients: q_1,q_2,...): (Show/hide table) [ Help ]
| Wave vector code | q_x | q_y | q_z |
|---|---|---|---|
| 1 | 0.00000 | 0.07143 | 0.00000 |
| 2 | 0.00000 | 0.14286 | 0.00000 |
| 3 | 0.00000 | 0.21429 | 0.00000 |
| 4 | 0.00000 | 0.28572 | 0.00000 |
| 5 | 0.00000 | 0.35715 | 0.00000 |
| 6 | 0.00000 | 0.42858 | 0.00000 |
| 7 | 0.00000 | 0.50001 | 0.00000 |
| 8 | 0.00000 | 0.57144 | 0.00000 |
| 9 | 0.00000 | 0.64287 | 0.00000 |
| 10 | 0.00000 | 0.71430 | 0.00000 |
| 11 | 0.00000 | 0.78573 | 0.00000 |
| 12 | 0.00000 | 0.85716 | 0.00000 |
Definition of the displacive (translational) Fourier series: (Show/hide table) [ Help ]
| Modulation code | Atom site label | Displacement axis | Wave vector code |
|---|---|---|---|
| Ca1x1 | Ca1 | x | 1 |
| Ca1y1 | Ca1 | y | 1 |
| Ca1z1 | Ca1 | z | 1 |
| Nb11x1 | Nb11 | x | 1 |
| Nb11y1 | Nb11 | y | 1 |
| Nb11z1 | Nb11 | z | 1 |
| Nb11x2 | Nb11 | x | 2 |
| Nb11y2 | Nb11 | y | 2 |
| Nb11z2 | Nb11 | z | 2 |
| Nb11x3 | Nb11 | x | 3 |
| Nb11y3 | Nb11 | y | 3 |
| Nb11z3 | Nb11 | z | 3 |
| Nb11x4 | Nb11 | x | 4 |
| Nb11y4 | Nb11 | y | 4 |
| Nb11z4 | Nb11 | z | 4 |
| Nb11x5 | Nb11 | x | 5 |
| Nb11y5 | Nb11 | y | 5 |
| Nb11z5 | Nb11 | z | 5 |
| Nb11x6 | Nb11 | x | 6 |
| Nb11y6 | Nb11 | y | 6 |
| Nb11z6 | Nb11 | z | 6 |
| Nb11x7 | Nb11 | x | 7 |
| Nb11y7 | Nb11 | y | 7 |
| Nb11z7 | Nb11 | z | 7 |
| Nb11x8 | Nb11 | x | 8 |
| Nb11y8 | Nb11 | y | 8 |
| Nb11z8 | Nb11 | z | 8 |
| Nb11x9 | Nb11 | x | 9 |
| Nb11y9 | Nb11 | y | 9 |
| Nb11z9 | Nb11 | z | 9 |
| Nb11x10 | Nb11 | x | 10 |
| Nb11y10 | Nb11 | y | 10 |
| Nb11z10 | Nb11 | z | 10 |
| Nb11x11 | Nb11 | x | 11 |
| Nb11y11 | Nb11 | y | 11 |
| Nb11z11 | Nb11 | z | 11 |
| Nb11x12 | Nb11 | x | 12 |
| Nb11y12 | Nb11 | y | 12 |
| Nb11z12 | Nb11 | z | 12 |
| Ti11x1 | Ti11 | x | 1 |
| Ti11y1 | Ti11 | y | 1 |
| Ti11z1 | Ti11 | z | 1 |
| Ti11x2 | Ti11 | x | 2 |
| Ti11y2 | Ti11 | y | 2 |
| Ti11z2 | Ti11 | z | 2 |
| Ti11x3 | Ti11 | x | 3 |
| Ti11y3 | Ti11 | y | 3 |
| Ti11z3 | Ti11 | z | 3 |
| Ti11x4 | Ti11 | x | 4 |
| Ti11y4 | Ti11 | y | 4 |
| Ti11z4 | Ti11 | z | 4 |
| Ti11x5 | Ti11 | x | 5 |
| Ti11y5 | Ti11 | y | 5 |
| Ti11z5 | Ti11 | z | 5 |
| Ti11x6 | Ti11 | x | 6 |
| Ti11y6 | Ti11 | y | 6 |
| Ti11z6 | Ti11 | z | 6 |
| Ti11x7 | Ti11 | x | 7 |
| Ti11y7 | Ti11 | y | 7 |
| Ti11z7 | Ti11 | z | 7 |
| Ti11x8 | Ti11 | x | 8 |
| Ti11y8 | Ti11 | y | 8 |
| Ti11z8 | Ti11 | z | 8 |
| Ti11x9 | Ti11 | x | 9 |
| Ti11y9 | Ti11 | y | 9 |
| Ti11z9 | Ti11 | z | 9 |
| Ti11x10 | Ti11 | x | 10 |
| Ti11y10 | Ti11 | y | 10 |
| Ti11z10 | Ti11 | z | 10 |
| Ti11x11 | Ti11 | x | 11 |
| Ti11y11 | Ti11 | y | 11 |
| Ti11z11 | Ti11 | z | 11 |
| Ti11x12 | Ti11 | x | 12 |
| Ti11y12 | Ti11 | y | 12 |
| Ti11z12 | Ti11 | z | 12 |
| Nb12x1 | Nb12 | x | 1 |
| Nb12y1 | Nb12 | y | 1 |
| Nb12z1 | Nb12 | z | 1 |
| Nb12x2 | Nb12 | x | 2 |
| Nb12y2 | Nb12 | y | 2 |
| Nb12z2 | Nb12 | z | 2 |
| Nb12x3 | Nb12 | x | 3 |
| Nb12y3 | Nb12 | y | 3 |
| Nb12z3 | Nb12 | z | 3 |
| Nb12x4 | Nb12 | x | 4 |
| Nb12y4 | Nb12 | y | 4 |
| Nb12z4 | Nb12 | z | 4 |
| Nb12x5 | Nb12 | x | 5 |
| Nb12y5 | Nb12 | y | 5 |
| Nb12z5 | Nb12 | z | 5 |
| Nb12x6 | Nb12 | x | 6 |
| Nb12y6 | Nb12 | y | 6 |
| Nb12z6 | Nb12 | z | 6 |
| Nb12x7 | Nb12 | x | 7 |
| Nb12y7 | Nb12 | y | 7 |
| Nb12z7 | Nb12 | z | 7 |
| Nb12x8 | Nb12 | x | 8 |
| Nb12y8 | Nb12 | y | 8 |
| Nb12z8 | Nb12 | z | 8 |
| Nb12x9 | Nb12 | x | 9 |
| Nb12y9 | Nb12 | y | 9 |
| Nb12z9 | Nb12 | z | 9 |
| Nb12x10 | Nb12 | x | 10 |
| Nb12y10 | Nb12 | y | 10 |
| Nb12z10 | Nb12 | z | 10 |
| Nb12x11 | Nb12 | x | 11 |
| Nb12y11 | Nb12 | y | 11 |
| Nb12z11 | Nb12 | z | 11 |
| Nb12x12 | Nb12 | x | 12 |
| Nb12y12 | Nb12 | y | 12 |
| Nb12z12 | Nb12 | z | 12 |
| Ti12x1 | Ti12 | x | 1 |
| Ti12y1 | Ti12 | y | 1 |
| Ti12z1 | Ti12 | z | 1 |
| Ti12x2 | Ti12 | x | 2 |
| Ti12y2 | Ti12 | y | 2 |
| Ti12z2 | Ti12 | z | 2 |
| Ti12x3 | Ti12 | x | 3 |
| Ti12y3 | Ti12 | y | 3 |
| Ti12z3 | Ti12 | z | 3 |
| Ti12x4 | Ti12 | x | 4 |
| Ti12y4 | Ti12 | y | 4 |
| Ti12z4 | Ti12 | z | 4 |
| Ti12x5 | Ti12 | x | 5 |
| Ti12y5 | Ti12 | y | 5 |
| Ti12z5 | Ti12 | z | 5 |
| Ti12x6 | Ti12 | x | 6 |
| Ti12y6 | Ti12 | y | 6 |
| Ti12z6 | Ti12 | z | 6 |
| Ti12x7 | Ti12 | x | 7 |
| Ti12y7 | Ti12 | y | 7 |
| Ti12z7 | Ti12 | z | 7 |
| Ti12x8 | Ti12 | x | 8 |
| Ti12y8 | Ti12 | y | 8 |
| Ti12z8 | Ti12 | z | 8 |
| Ti12x9 | Ti12 | x | 9 |
| Ti12y9 | Ti12 | y | 9 |
| Ti12z9 | Ti12 | z | 9 |
| Ti12x10 | Ti12 | x | 10 |
| Ti12y10 | Ti12 | y | 10 |
| Ti12z10 | Ti12 | z | 10 |
| Ti12x11 | Ti12 | x | 11 |
| Ti12y11 | Ti12 | y | 11 |
| Ti12z11 | Ti12 | z | 11 |
| Ti12x12 | Ti12 | x | 12 |
| Ti12y12 | Ti12 | y | 12 |
| Ti12z12 | Ti12 | z | 12 |
| Nb13x1 | Nb13 | x | 1 |
| Nb13y1 | Nb13 | y | 1 |
| Nb13z1 | Nb13 | z | 1 |
| Nb13x2 | Nb13 | x | 2 |
| Nb13y2 | Nb13 | y | 2 |
| Nb13z2 | Nb13 | z | 2 |
| Nb13x3 | Nb13 | x | 3 |
| Nb13y3 | Nb13 | y | 3 |
| Nb13z3 | Nb13 | z | 3 |
| Nb13x4 | Nb13 | x | 4 |
| Nb13y4 | Nb13 | y | 4 |
| Nb13z4 | Nb13 | z | 4 |
| Nb13x5 | Nb13 | x | 5 |
| Nb13y5 | Nb13 | y | 5 |
| Nb13z5 | Nb13 | z | 5 |
| Nb13x6 | Nb13 | x | 6 |
| Nb13y6 | Nb13 | y | 6 |
| Nb13z6 | Nb13 | z | 6 |
| Nb13x7 | Nb13 | x | 7 |
| Nb13y7 | Nb13 | y | 7 |
| Nb13z7 | Nb13 | z | 7 |
| Nb13x8 | Nb13 | x | 8 |
| Nb13y8 | Nb13 | y | 8 |
| Nb13z8 | Nb13 | z | 8 |
| Nb13x9 | Nb13 | x | 9 |
| Nb13y9 | Nb13 | y | 9 |
| Nb13z9 | Nb13 | z | 9 |
| Nb13x10 | Nb13 | x | 10 |
| Nb13y10 | Nb13 | y | 10 |
| Nb13z10 | Nb13 | z | 10 |
| Nb13x11 | Nb13 | x | 11 |
| Nb13y11 | Nb13 | y | 11 |
| Nb13z11 | Nb13 | z | 11 |
| Nb13x12 | Nb13 | x | 12 |
| Nb13y12 | Nb13 | y | 12 |
| Nb13z12 | Nb13 | z | 12 |
| Ti13x1 | Ti13 | x | 1 |
| Ti13y1 | Ti13 | y | 1 |
| Ti13z1 | Ti13 | z | 1 |
| Ti13x2 | Ti13 | x | 2 |
| Ti13y2 | Ti13 | y | 2 |
| Ti13z2 | Ti13 | z | 2 |
| Ti13x3 | Ti13 | x | 3 |
| Ti13y3 | Ti13 | y | 3 |
| Ti13z3 | Ti13 | z | 3 |
| Ti13x4 | Ti13 | x | 4 |
| Ti13y4 | Ti13 | y | 4 |
| Ti13z4 | Ti13 | z | 4 |
| Ti13x5 | Ti13 | x | 5 |
| Ti13y5 | Ti13 | y | 5 |
| Ti13z5 | Ti13 | z | 5 |
| Ti13x6 | Ti13 | x | 6 |
| Ti13y6 | Ti13 | y | 6 |
| Ti13z6 | Ti13 | z | 6 |
| Ti13x7 | Ti13 | x | 7 |
| Ti13y7 | Ti13 | y | 7 |
| Ti13z7 | Ti13 | z | 7 |
| Ti13x8 | Ti13 | x | 8 |
| Ti13y8 | Ti13 | y | 8 |
| Ti13z8 | Ti13 | z | 8 |
| Ti13x9 | Ti13 | x | 9 |
| Ti13y9 | Ti13 | y | 9 |
| Ti13z9 | Ti13 | z | 9 |
| Ti13x10 | Ti13 | x | 10 |
| Ti13y10 | Ti13 | y | 10 |
| Ti13z10 | Ti13 | z | 10 |
| Ti13x11 | Ti13 | x | 11 |
| Ti13y11 | Ti13 | y | 11 |
| Ti13z11 | Ti13 | z | 11 |
| Ti13x12 | Ti13 | x | 12 |
| Ti13y12 | Ti13 | y | 12 |
| Ti13z12 | Ti13 | z | 12 |
| Nb21x1 | Nb21 | x | 1 |
| Nb21y1 | Nb21 | y | 1 |
| Nb21z1 | Nb21 | z | 1 |
| Nb21x2 | Nb21 | x | 2 |
| Nb21y2 | Nb21 | y | 2 |
| Nb21z2 | Nb21 | z | 2 |
| Nb21x3 | Nb21 | x | 3 |
| Nb21y3 | Nb21 | y | 3 |
| Nb21z3 | Nb21 | z | 3 |
| Nb21x4 | Nb21 | x | 4 |
| Nb21y4 | Nb21 | y | 4 |
| Nb21z4 | Nb21 | z | 4 |
| Nb21x5 | Nb21 | x | 5 |
| Nb21y5 | Nb21 | y | 5 |
| Nb21z5 | Nb21 | z | 5 |
| Nb21x6 | Nb21 | x | 6 |
| Nb21y6 | Nb21 | y | 6 |
| Nb21z6 | Nb21 | z | 6 |
| Nb21x7 | Nb21 | x | 7 |
| Nb21y7 | Nb21 | y | 7 |
| Nb21z7 | Nb21 | z | 7 |
| Nb21x8 | Nb21 | x | 8 |
| Nb21y8 | Nb21 | y | 8 |
| Nb21z8 | Nb21 | z | 8 |
| Nb21x9 | Nb21 | x | 9 |
| Nb21y9 | Nb21 | y | 9 |
| Nb21z9 | Nb21 | z | 9 |
| Nb21x10 | Nb21 | x | 10 |
| Nb21y10 | Nb21 | y | 10 |
| Nb21z10 | Nb21 | z | 10 |
| Nb21x11 | Nb21 | x | 11 |
| Nb21y11 | Nb21 | y | 11 |
| Nb21z11 | Nb21 | z | 11 |
| Nb21x12 | Nb21 | x | 12 |
| Nb21y12 | Nb21 | y | 12 |
| Nb21z12 | Nb21 | z | 12 |
| Ti21x1 | Ti21 | x | 1 |
| Ti21y1 | Ti21 | y | 1 |
| Ti21z1 | Ti21 | z | 1 |
| Ti21x2 | Ti21 | x | 2 |
| Ti21y2 | Ti21 | y | 2 |
| Ti21z2 | Ti21 | z | 2 |
| Ti21x3 | Ti21 | x | 3 |
| Ti21y3 | Ti21 | y | 3 |
| Ti21z3 | Ti21 | z | 3 |
| Ti21x4 | Ti21 | x | 4 |
| Ti21y4 | Ti21 | y | 4 |
| Ti21z4 | Ti21 | z | 4 |
| Ti21x5 | Ti21 | x | 5 |
| Ti21y5 | Ti21 | y | 5 |
| Ti21z5 | Ti21 | z | 5 |
| Ti21x6 | Ti21 | x | 6 |
| Ti21y6 | Ti21 | y | 6 |
| Ti21z6 | Ti21 | z | 6 |
| Ti21x7 | Ti21 | x | 7 |
| Ti21y7 | Ti21 | y | 7 |
| Ti21z7 | Ti21 | z | 7 |
| Ti21x8 | Ti21 | x | 8 |
| Ti21y8 | Ti21 | y | 8 |
| Ti21z8 | Ti21 | z | 8 |
| Ti21x9 | Ti21 | x | 9 |
| Ti21y9 | Ti21 | y | 9 |
| Ti21z9 | Ti21 | z | 9 |
| Ti21x10 | Ti21 | x | 10 |
| Ti21y10 | Ti21 | y | 10 |
| Ti21z10 | Ti21 | z | 10 |
| Ti21x11 | Ti21 | x | 11 |
| Ti21y11 | Ti21 | y | 11 |
| Ti21z11 | Ti21 | z | 11 |
| Ti21x12 | Ti21 | x | 12 |
| Ti21y12 | Ti21 | y | 12 |
| Ti21z12 | Ti21 | z | 12 |
| Nb22x1 | Nb22 | x | 1 |
| Nb22y1 | Nb22 | y | 1 |
| Nb22z1 | Nb22 | z | 1 |
| Nb22x2 | Nb22 | x | 2 |
| Nb22y2 | Nb22 | y | 2 |
| Nb22z2 | Nb22 | z | 2 |
| Nb22x3 | Nb22 | x | 3 |
| Nb22y3 | Nb22 | y | 3 |
| Nb22z3 | Nb22 | z | 3 |
| Nb22x4 | Nb22 | x | 4 |
| Nb22y4 | Nb22 | y | 4 |
| Nb22z4 | Nb22 | z | 4 |
| Nb22x5 | Nb22 | x | 5 |
| Nb22y5 | Nb22 | y | 5 |
| Nb22z5 | Nb22 | z | 5 |
| Nb22x6 | Nb22 | x | 6 |
| Nb22y6 | Nb22 | y | 6 |
| Nb22z6 | Nb22 | z | 6 |
| Nb22x7 | Nb22 | x | 7 |
| Nb22y7 | Nb22 | y | 7 |
| Nb22z7 | Nb22 | z | 7 |
| Nb22x8 | Nb22 | x | 8 |
| Nb22y8 | Nb22 | y | 8 |
| Nb22z8 | Nb22 | z | 8 |
| Nb22x9 | Nb22 | x | 9 |
| Nb22y9 | Nb22 | y | 9 |
| Nb22z9 | Nb22 | z | 9 |
| Nb22x10 | Nb22 | x | 10 |
| Nb22y10 | Nb22 | y | 10 |
| Nb22z10 | Nb22 | z | 10 |
| Nb22x11 | Nb22 | x | 11 |
| Nb22y11 | Nb22 | y | 11 |
| Nb22z11 | Nb22 | z | 11 |
| Nb22x12 | Nb22 | x | 12 |
| Nb22y12 | Nb22 | y | 12 |
| Nb22z12 | Nb22 | z | 12 |
| Ti22x1 | Ti22 | x | 1 |
| Ti22y1 | Ti22 | y | 1 |
| Ti22z1 | Ti22 | z | 1 |
| Ti22x2 | Ti22 | x | 2 |
| Ti22y2 | Ti22 | y | 2 |
| Ti22z2 | Ti22 | z | 2 |
| Ti22x3 | Ti22 | x | 3 |
| Ti22y3 | Ti22 | y | 3 |
| Ti22z3 | Ti22 | z | 3 |
| Ti22x4 | Ti22 | x | 4 |
| Ti22y4 | Ti22 | y | 4 |
| Ti22z4 | Ti22 | z | 4 |
| Ti22x5 | Ti22 | x | 5 |
| Ti22y5 | Ti22 | y | 5 |
| Ti22z5 | Ti22 | z | 5 |
| Ti22x6 | Ti22 | x | 6 |
| Ti22y6 | Ti22 | y | 6 |
| Ti22z6 | Ti22 | z | 6 |
| Ti22x7 | Ti22 | x | 7 |
| Ti22y7 | Ti22 | y | 7 |
| Ti22z7 | Ti22 | z | 7 |
| Ti22x8 | Ti22 | x | 8 |
| Ti22y8 | Ti22 | y | 8 |
| Ti22z8 | Ti22 | z | 8 |
| Ti22x9 | Ti22 | x | 9 |
| Ti22y9 | Ti22 | y | 9 |
| Ti22z9 | Ti22 | z | 9 |
| Ti22x10 | Ti22 | x | 10 |
| Ti22y10 | Ti22 | y | 10 |
| Ti22z10 | Ti22 | z | 10 |
| Ti22x11 | Ti22 | x | 11 |
| Ti22y11 | Ti22 | y | 11 |
| Ti22z11 | Ti22 | z | 11 |
| Ti22x12 | Ti22 | x | 12 |
| Ti22y12 | Ti22 | y | 12 |
| Ti22z12 | Ti22 | z | 12 |
| Nb23x1 | Nb23 | x | 1 |
| Nb23y1 | Nb23 | y | 1 |
| Nb23z1 | Nb23 | z | 1 |
| Nb23x2 | Nb23 | x | 2 |
| Nb23y2 | Nb23 | y | 2 |
| Nb23z2 | Nb23 | z | 2 |
| Nb23x3 | Nb23 | x | 3 |
| Nb23y3 | Nb23 | y | 3 |
| Nb23z3 | Nb23 | z | 3 |
| Nb23x4 | Nb23 | x | 4 |
| Nb23y4 | Nb23 | y | 4 |
| Nb23z4 | Nb23 | z | 4 |
| Nb23x5 | Nb23 | x | 5 |
| Nb23y5 | Nb23 | y | 5 |
| Nb23z5 | Nb23 | z | 5 |
| Nb23x6 | Nb23 | x | 6 |
| Nb23y6 | Nb23 | y | 6 |
| Nb23z6 | Nb23 | z | 6 |
| Nb23x7 | Nb23 | x | 7 |
| Nb23y7 | Nb23 | y | 7 |
| Nb23z7 | Nb23 | z | 7 |
| Nb23x8 | Nb23 | x | 8 |
| Nb23y8 | Nb23 | y | 8 |
| Nb23z8 | Nb23 | z | 8 |
| Nb23x9 | Nb23 | x | 9 |
| Nb23y9 | Nb23 | y | 9 |
| Nb23z9 | Nb23 | z | 9 |
| Nb23x10 | Nb23 | x | 10 |
| Nb23y10 | Nb23 | y | 10 |
| Nb23z10 | Nb23 | z | 10 |
| Nb23x11 | Nb23 | x | 11 |
| Nb23y11 | Nb23 | y | 11 |
| Nb23z11 | Nb23 | z | 11 |
| Nb23x12 | Nb23 | x | 12 |
| Nb23y12 | Nb23 | y | 12 |
| Nb23z12 | Nb23 | z | 12 |
| Ti23x1 | Ti23 | x | 1 |
| Ti23y1 | Ti23 | y | 1 |
| Ti23z1 | Ti23 | z | 1 |
| Ti23x2 | Ti23 | x | 2 |
| Ti23y2 | Ti23 | y | 2 |
| Ti23z2 | Ti23 | z | 2 |
| Ti23x3 | Ti23 | x | 3 |
| Ti23y3 | Ti23 | y | 3 |
| Ti23z3 | Ti23 | z | 3 |
| Ti23x4 | Ti23 | x | 4 |
| Ti23y4 | Ti23 | y | 4 |
| Ti23z4 | Ti23 | z | 4 |
| Ti23x5 | Ti23 | x | 5 |
| Ti23y5 | Ti23 | y | 5 |
| Ti23z5 | Ti23 | z | 5 |
| Ti23x6 | Ti23 | x | 6 |
| Ti23y6 | Ti23 | y | 6 |
| Ti23z6 | Ti23 | z | 6 |
| Ti23x7 | Ti23 | x | 7 |
| Ti23y7 | Ti23 | y | 7 |
| Ti23z7 | Ti23 | z | 7 |
| Ti23x8 | Ti23 | x | 8 |
| Ti23y8 | Ti23 | y | 8 |
| Ti23z8 | Ti23 | z | 8 |
| Ti23x9 | Ti23 | x | 9 |
| Ti23y9 | Ti23 | y | 9 |
| Ti23z9 | Ti23 | z | 9 |
| Ti23x10 | Ti23 | x | 10 |
| Ti23y10 | Ti23 | y | 10 |
| Ti23z10 | Ti23 | z | 10 |
| Ti23x11 | Ti23 | x | 11 |
| Ti23y11 | Ti23 | y | 11 |
| Ti23z11 | Ti23 | z | 11 |
| Ti23x12 | Ti23 | x | 12 |
| Ti23y12 | Ti23 | y | 12 |
| Ti23z12 | Ti23 | z | 12 |
| O1x1 | O1 | x | 1 |
| O1y1 | O1 | y | 1 |
| O1z1 | O1 | z | 1 |
| O1x2 | O1 | x | 2 |
| O1y2 | O1 | y | 2 |
| O1z2 | O1 | z | 2 |
| O1x3 | O1 | x | 3 |
| O1y3 | O1 | y | 3 |
| O1z3 | O1 | z | 3 |
| O2x1 | O2 | x | 1 |
| O2y1 | O2 | y | 1 |
| O2z1 | O2 | z | 1 |
| O2x2 | O2 | x | 2 |
| O2y2 | O2 | y | 2 |
| O2z2 | O2 | z | 2 |
| O2x3 | O2 | x | 3 |
| O2y3 | O2 | y | 3 |
| O2z3 | O2 | z | 3 |
| O3x1 | O3 | x | 1 |
| O3y1 | O3 | y | 1 |
| O3z1 | O3 | z | 1 |
| O3x2 | O3 | x | 2 |
| O3y2 | O3 | y | 2 |
| O3z2 | O3 | z | 2 |
| O3x3 | O3 | x | 3 |
| O3y3 | O3 | y | 3 |
| O3z3 | O3 | z | 3 |
Displacive (translational) Fourier coefficients: (Show/hide table) [ Help ]
| Modulation code | Cosine coefficient | Sine coefficient |
|---|---|---|
| Ca1x1 | 0.00005(11) | 0.00073(18) |
| Ca1y1 | 0.00011(12) | 0.02417(12) |
| Ca1z1 | 0.00199(16) | -0.00088(16) |
| Nb11x1 | 0 | -0.0015(2) |
| Nb11y1 | 0 | 0.12492(16) |
| Nb11z1 | 0 | -0.0375(3) |
| Nb11x2 | 0 | 0 |
| Nb11y2 | 0 | 0 |
| Nb11z2 | 0 | 0 |
| Nb11x3 | 0 | 0 |
| Nb11y3 | 0 | 0 |
| Nb11z3 | 0 | 0 |
| Nb11x4 | 0 | 0 |
| Nb11y4 | 0 | 0 |
| Nb11z4 | 0 | 0 |
| Nb11x5 | 0 | 0 |
| Nb11y5 | 0 | 0 |
| Nb11z5 | 0 | 0 |
| Nb11x6 | 0 | 0.00145(14) |
| Nb11y6 | 0 | 0.00397(10) |
| Nb11z6 | 0 | 0.01159(17) |
| Nb11x7 | 0 | 0 |
| Nb11y7 | 0 | 0 |
| Nb11z7 | 0 | 0 |
| Nb11x8 | 0 | 0 |
| Nb11y8 | 0 | 0 |
| Nb11z8 | 0 | 0 |
| Nb11x9 | 0 | 0 |
| Nb11y9 | 0 | 0 |
| Nb11z9 | 0 | 0 |
| Nb11x10 | 0 | 0 |
| Nb11y10 | 0 | 0 |
| Nb11z10 | 0 | 0 |
| Nb11x11 | 0 | 0 |
| Nb11y11 | 0 | 0 |
| Nb11z11 | 0 | 0 |
| Nb11x12 | 0 | -0.00181(12) |
| Nb11y12 | 0 | -0.00666(10) |
| Nb11z12 | 0 | -0.0089(3) |
| Ti11x1 | 0 | -0.0015(2) |
| Ti11y1 | 0 | 0.12492(16) |
| Ti11z1 | 0 | -0.0375(3) |
| Ti11x2 | 0 | 0 |
| Ti11y2 | 0 | 0 |
| Ti11z2 | 0 | 0 |
| Ti11x3 | 0 | 0 |
| Ti11y3 | 0 | 0 |
| Ti11z3 | 0 | 0 |
| Ti11x4 | 0 | 0 |
| Ti11y4 | 0 | 0 |
| Ti11z4 | 0 | 0 |
| Ti11x5 | 0 | 0 |
| Ti11y5 | 0 | 0 |
| Ti11z5 | 0 | 0 |
| Ti11x6 | 0 | 0.00145(14) |
| Ti11y6 | 0 | 0.00397(10) |
| Ti11z6 | 0 | 0.01159(17) |
| Ti11x7 | 0 | 0 |
| Ti11y7 | 0 | 0 |
| Ti11z7 | 0 | 0 |
| Ti11x8 | 0 | 0 |
| Ti11y8 | 0 | 0 |
| Ti11z8 | 0 | 0 |
| Ti11x9 | 0 | 0 |
| Ti11y9 | 0 | 0 |
| Ti11z9 | 0 | 0 |
| Ti11x10 | 0 | 0 |
| Ti11y10 | 0 | 0 |
| Ti11z10 | 0 | 0 |
| Ti11x11 | 0 | 0 |
| Ti11y11 | 0 | 0 |
| Ti11z11 | 0 | 0 |
| Ti11x12 | 0 | -0.00181(12) |
| Ti11y12 | 0 | -0.00666(10) |
| Ti11z12 | 0 | -0.0089(3) |
| Nb12x1 | 0 | -0.0015(2) |
| Nb12y1 | 0 | 0.12492(16) |
| Nb12z1 | 0 | -0.0375(3) |
| Nb12x2 | 0 | 0 |
| Nb12y2 | 0 | 0 |
| Nb12z2 | 0 | 0 |
| Nb12x3 | 0 | 0 |
| Nb12y3 | 0 | 0 |
| Nb12z3 | 0 | 0 |
| Nb12x4 | 0 | 0 |
| Nb12y4 | 0 | 0 |
| Nb12z4 | 0 | 0 |
| Nb12x5 | 0 | 0 |
| Nb12y5 | 0 | 0 |
| Nb12z5 | 0 | 0 |
| Nb12x6 | 0 | 0.00145(14) |
| Nb12y6 | 0 | 0.00397(10) |
| Nb12z6 | 0 | 0.01159(17) |
| Nb12x7 | 0 | 0 |
| Nb12y7 | 0 | 0 |
| Nb12z7 | 0 | 0 |
| Nb12x8 | 0 | 0 |
| Nb12y8 | 0 | 0 |
| Nb12z8 | 0 | 0 |
| Nb12x9 | 0 | 0 |
| Nb12y9 | 0 | 0 |
| Nb12z9 | 0 | 0 |
| Nb12x10 | 0 | 0 |
| Nb12y10 | 0 | 0 |
| Nb12z10 | 0 | 0 |
| Nb12x11 | 0 | 0 |
| Nb12y11 | 0 | 0 |
| Nb12z11 | 0 | 0 |
| Nb12x12 | 0 | -0.00181(12) |
| Nb12y12 | 0 | -0.00666(10) |
| Nb12z12 | 0 | -0.0089(3) |
| Ti12x1 | 0 | -0.0015(2) |
| Ti12y1 | 0 | 0.12492(16) |
| Ti12z1 | 0 | -0.0375(3) |
| Ti12x2 | 0 | 0 |
| Ti12y2 | 0 | 0 |
| Ti12z2 | 0 | 0 |
| Ti12x3 | 0 | 0 |
| Ti12y3 | 0 | 0 |
| Ti12z3 | 0 | 0 |
| Ti12x4 | 0 | 0 |
| Ti12y4 | 0 | 0 |
| Ti12z4 | 0 | 0 |
| Ti12x5 | 0 | 0 |
| Ti12y5 | 0 | 0 |
| Ti12z5 | 0 | 0 |
| Ti12x6 | 0 | 0.00145(14) |
| Ti12y6 | 0 | 0.00397(10) |
| Ti12z6 | 0 | 0.01159(17) |
| Ti12x7 | 0 | 0 |
| Ti12y7 | 0 | 0 |
| Ti12z7 | 0 | 0 |
| Ti12x8 | 0 | 0 |
| Ti12y8 | 0 | 0 |
| Ti12z8 | 0 | 0 |
| Ti12x9 | 0 | 0 |
| Ti12y9 | 0 | 0 |
| Ti12z9 | 0 | 0 |
| Ti12x10 | 0 | 0 |
| Ti12y10 | 0 | 0 |
| Ti12z10 | 0 | 0 |
| Ti12x11 | 0 | 0 |
| Ti12y11 | 0 | 0 |
| Ti12z11 | 0 | 0 |
| Ti12x12 | 0 | -0.00181(12) |
| Ti12y12 | 0 | -0.00666(10) |
| Ti12z12 | 0 | -0.0089(3) |
| Nb13x1 | 0 | -0.0015(2) |
| Nb13y1 | 0 | 0.12492(16) |
| Nb13z1 | 0 | -0.0375(3) |
| Nb13x2 | 0 | 0 |
| Nb13y2 | 0 | 0 |
| Nb13z2 | 0 | 0 |
| Nb13x3 | 0 | 0 |
| Nb13y3 | 0 | 0 |
| Nb13z3 | 0 | 0 |
| Nb13x4 | 0 | 0 |
| Nb13y4 | 0 | 0 |
| Nb13z4 | 0 | 0 |
| Nb13x5 | 0 | 0 |
| Nb13y5 | 0 | 0 |
| Nb13z5 | 0 | 0 |
| Nb13x6 | 0 | 0.00145(14) |
| Nb13y6 | 0 | 0.00397(10) |
| Nb13z6 | 0 | 0.01157(17) |
| Nb13x7 | 0 | 0 |
| Nb13y7 | 0 | 0 |
| Nb13z7 | 0 | 0 |
| Nb13x8 | 0 | 0 |
| Nb13y8 | 0 | 0 |
| Nb13z8 | 0 | 0 |
| Nb13x9 | 0 | 0 |
| Nb13y9 | 0 | 0 |
| Nb13z9 | 0 | 0 |
| Nb13x10 | 0 | 0 |
| Nb13y10 | 0 | 0 |
| Nb13z10 | 0 | 0 |
| Nb13x11 | 0 | 0 |
| Nb13y11 | 0 | 0 |
| Nb13z11 | 0 | 0 |
| Nb13x12 | 0 | -0.00181(12) |
| Nb13y12 | 0 | -0.00666(10) |
| Nb13z12 | 0 | -0.0089(3) |
| Ti13x1 | 0 | -0.0015(2) |
| Ti13y1 | 0 | 0.12492(16) |
| Ti13z1 | 0 | -0.0375(3) |
| Ti13x2 | 0 | 0 |
| Ti13y2 | 0 | 0 |
| Ti13z2 | 0 | 0 |
| Ti13x3 | 0 | 0 |
| Ti13y3 | 0 | 0 |
| Ti13z3 | 0 | 0 |
| Ti13x4 | 0 | 0 |
| Ti13y4 | 0 | 0 |
| Ti13z4 | 0 | 0 |
| Ti13x5 | 0 | 0 |
| Ti13y5 | 0 | 0 |
| Ti13z5 | 0 | 0 |
| Ti13x6 | 0 | 0.00145(14) |
| Ti13y6 | 0 | 0.00397(10) |
| Ti13z6 | 0 | 0.01157(17) |
| Ti13x7 | 0 | 0 |
| Ti13y7 | 0 | 0 |
| Ti13z7 | 0 | 0 |
| Ti13x8 | 0 | 0 |
| Ti13y8 | 0 | 0 |
| Ti13z8 | 0 | 0 |
| Ti13x9 | 0 | 0 |
| Ti13y9 | 0 | 0 |
| Ti13z9 | 0 | 0 |
| Ti13x10 | 0 | 0 |
| Ti13y10 | 0 | 0 |
| Ti13z10 | 0 | 0 |
| Ti13x11 | 0 | 0 |
| Ti13y11 | 0 | 0 |
| Ti13z11 | 0 | 0 |
| Ti13x12 | 0 | -0.00181(12) |
| Ti13y12 | 0 | -0.00666(10) |
| Ti13z12 | 0 | -0.0089(3) |
| Nb21x1 | 0 | 0.0098(2) |
| Nb21y1 | 0 | 0.13601(17) |
| Nb21z1 | 0 | -0.0433(3) |
| Nb21x2 | 0 | 0 |
| Nb21y2 | 0 | 0 |
| Nb21z2 | 0 | 0 |
| Nb21x3 | 0 | 0 |
| Nb21y3 | 0 | 0 |
| Nb21z3 | 0 | 0 |
| Nb21x4 | 0 | 0 |
| Nb21y4 | 0 | 0 |
| Nb21z4 | 0 | 0 |
| Nb21x5 | 0 | 0 |
| Nb21y5 | 0 | 0 |
| Nb21z5 | 0 | 0 |
| Nb21x6 | 0 | -0.00320(14) |
| Nb21y6 | 0 | 0.00465(10) |
| Nb21z6 | 0 | 0.01252(17) |
| Nb21x7 | 0 | 0 |
| Nb21y7 | 0 | 0 |
| Nb21z7 | 0 | 0 |
| Nb21x8 | 0 | 0 |
| Nb21y8 | 0 | 0 |
| Nb21z8 | 0 | 0 |
| Nb21x9 | 0 | 0 |
| Nb21y9 | 0 | 0 |
| Nb21z9 | 0 | 0 |
| Nb21x10 | 0 | 0 |
| Nb21y10 | 0 | 0 |
| Nb21z10 | 0 | 0 |
| Nb21x11 | 0 | 0 |
| Nb21y11 | 0 | 0 |
| Nb21z11 | 0 | 0 |
| Nb21x12 | 0 | 0.00185(11) |
| Nb21y12 | 0 | -0.00664(10) |
| Nb21z12 | 0 | -0.0091(3) |
| Ti21x1 | 0 | 0.0098(2) |
| Ti21y1 | 0 | 0.13601(17) |
| Ti21z1 | 0 | -0.0433(3) |
| Ti21x2 | 0 | 0 |
| Ti21y2 | 0 | 0 |
| Ti21z2 | 0 | 0 |
| Ti21x3 | 0 | 0 |
| Ti21y3 | 0 | 0 |
| Ti21z3 | 0 | 0 |
| Ti21x4 | 0 | 0 |
| Ti21y4 | 0 | 0 |
| Ti21z4 | 0 | 0 |
| Ti21x5 | 0 | 0 |
| Ti21y5 | 0 | 0 |
| Ti21z5 | 0 | 0 |
| Ti21x6 | 0 | -0.00320(14) |
| Ti21y6 | 0 | 0.00465(10) |
| Ti21z6 | 0 | 0.01252(17) |
| Ti21x7 | 0 | 0 |
| Ti21y7 | 0 | 0 |
| Ti21z7 | 0 | 0 |
| Ti21x8 | 0 | 0 |
| Ti21y8 | 0 | 0 |
| Ti21z8 | 0 | 0 |
| Ti21x9 | 0 | 0 |
| Ti21y9 | 0 | 0 |
| Ti21z9 | 0 | 0 |
| Ti21x10 | 0 | 0 |
| Ti21y10 | 0 | 0 |
| Ti21z10 | 0 | 0 |
| Ti21x11 | 0 | 0 |
| Ti21y11 | 0 | 0 |
| Ti21z11 | 0 | 0 |
| Ti21x12 | 0 | 0.00185(11) |
| Ti21y12 | 0 | -0.00664(10) |
| Ti21z12 | 0 | -0.0091(3) |
| Nb22x1 | 0 | 0.0098(2) |
| Nb22y1 | 0 | 0.13601(17) |
| Nb22z1 | 0 | -0.0433(3) |
| Nb22x2 | 0 | 0 |
| Nb22y2 | 0 | 0 |
| Nb22z2 | 0 | 0 |
| Nb22x3 | 0 | 0 |
| Nb22y3 | 0 | 0 |
| Nb22z3 | 0 | 0 |
| Nb22x4 | 0 | 0 |
| Nb22y4 | 0 | 0 |
| Nb22z4 | 0 | 0 |
| Nb22x5 | 0 | 0 |
| Nb22y5 | 0 | 0 |
| Nb22z5 | 0 | 0 |
| Nb22x6 | 0 | -0.00320(14) |
| Nb22y6 | 0 | 0.00465(10) |
| Nb22z6 | 0 | 0.01252(17) |
| Nb22x7 | 0 | 0 |
| Nb22y7 | 0 | 0 |
| Nb22z7 | 0 | 0 |
| Nb22x8 | 0 | 0 |
| Nb22y8 | 0 | 0 |
| Nb22z8 | 0 | 0 |
| Nb22x9 | 0 | 0 |
| Nb22y9 | 0 | 0 |
| Nb22z9 | 0 | 0 |
| Nb22x10 | 0 | 0 |
| Nb22y10 | 0 | 0 |
| Nb22z10 | 0 | 0 |
| Nb22x11 | 0 | 0 |
| Nb22y11 | 0 | 0 |
| Nb22z11 | 0 | 0 |
| Nb22x12 | 0 | 0.00185(11) |
| Nb22y12 | 0 | -0.00664(10) |
| Nb22z12 | 0 | -0.0091(3) |
| Ti22x1 | 0 | 0.0098(2) |
| Ti22y1 | 0 | 0.13601(17) |
| Ti22z1 | 0 | -0.0433(3) |
| Ti22x2 | 0 | 0 |
| Ti22y2 | 0 | 0 |
| Ti22z2 | 0 | 0 |
| Ti22x3 | 0 | 0 |
| Ti22y3 | 0 | 0 |
| Ti22z3 | 0 | 0 |
| Ti22x4 | 0 | 0 |
| Ti22y4 | 0 | 0 |
| Ti22z4 | 0 | 0 |
| Ti22x5 | 0 | 0 |
| Ti22y5 | 0 | 0 |
| Ti22z5 | 0 | 0 |
| Ti22x6 | 0 | -0.00320(14) |
| Ti22y6 | 0 | 0.00465(10) |
| Ti22z6 | 0 | 0.01252(17) |
| Ti22x7 | 0 | 0 |
| Ti22y7 | 0 | 0 |
| Ti22z7 | 0 | 0 |
| Ti22x8 | 0 | 0 |
| Ti22y8 | 0 | 0 |
| Ti22z8 | 0 | 0 |
| Ti22x9 | 0 | 0 |
| Ti22y9 | 0 | 0 |
| Ti22z9 | 0 | 0 |
| Ti22x10 | 0 | 0 |
| Ti22y10 | 0 | 0 |
| Ti22z10 | 0 | 0 |
| Ti22x11 | 0 | 0 |
| Ti22y11 | 0 | 0 |
| Ti22z11 | 0 | 0 |
| Ti22x12 | 0 | 0.00185(11) |
| Ti22y12 | 0 | -0.00664(10) |
| Ti22z12 | 0 | -0.0091(3) |
| Nb23x1 | 0 | 0.0098(2) |
| Nb23y1 | 0 | 0.13601(17) |
| Nb23z1 | 0 | -0.0433(3) |
| Nb23x2 | 0 | 0 |
| Nb23y2 | 0 | 0 |
| Nb23z2 | 0 | 0 |
| Nb23x3 | 0 | 0 |
| Nb23y3 | 0 | 0 |
| Nb23z3 | 0 | 0 |
| Nb23x4 | 0 | 0 |
| Nb23y4 | 0 | 0 |
| Nb23z4 | 0 | 0 |
| Nb23x5 | 0 | 0 |
| Nb23y5 | 0 | 0 |
| Nb23z5 | 0 | 0 |
| Nb23x6 | 0 | -0.00321(14) |
| Nb23y6 | 0 | 0.00465(10) |
| Nb23z6 | 0 | 0.01250(17) |
| Nb23x7 | 0 | 0 |
| Nb23y7 | 0 | 0 |
| Nb23z7 | 0 | 0 |
| Nb23x8 | 0 | 0 |
| Nb23y8 | 0 | 0 |
| Nb23z8 | 0 | 0 |
| Nb23x9 | 0 | 0 |
| Nb23y9 | 0 | 0 |
| Nb23z9 | 0 | 0 |
| Nb23x10 | 0 | 0 |
| Nb23y10 | 0 | 0 |
| Nb23z10 | 0 | 0 |
| Nb23x11 | 0 | 0 |
| Nb23y11 | 0 | 0 |
| Nb23z11 | 0 | 0 |
| Nb23x12 | 0 | 0.00186(11) |
| Nb23y12 | 0 | -0.00664(10) |
| Nb23z12 | 0 | -0.0090(3) |
| Ti23x1 | 0 | 0.0098(2) |
| Ti23y1 | 0 | 0.13601(17) |
| Ti23z1 | 0 | -0.0433(3) |
| Ti23x2 | 0 | 0 |
| Ti23y2 | 0 | 0 |
| Ti23z2 | 0 | 0 |
| Ti23x3 | 0 | 0 |
| Ti23y3 | 0 | 0 |
| Ti23z3 | 0 | 0 |
| Ti23x4 | 0 | 0 |
| Ti23y4 | 0 | 0 |
| Ti23z4 | 0 | 0 |
| Ti23x5 | 0 | 0 |
| Ti23y5 | 0 | 0 |
| Ti23z5 | 0 | 0 |
| Ti23x6 | 0 | -0.00321(14) |
| Ti23y6 | 0 | 0.00465(10) |
| Ti23z6 | 0 | 0.01250(17) |
| Ti23x7 | 0 | 0 |
| Ti23y7 | 0 | 0 |
| Ti23z7 | 0 | 0 |
| Ti23x8 | 0 | 0 |
| Ti23y8 | 0 | 0 |
| Ti23z8 | 0 | 0 |
| Ti23x9 | 0 | 0 |
| Ti23y9 | 0 | 0 |
| Ti23z9 | 0 | 0 |
| Ti23x10 | 0 | 0 |
| Ti23y10 | 0 | 0 |
| Ti23z10 | 0 | 0 |
| Ti23x11 | 0 | 0 |
| Ti23y11 | 0 | 0 |
| Ti23z11 | 0 | 0 |
| Ti23x12 | 0 | 0.00186(11) |
| Ti23y12 | 0 | -0.00664(10) |
| Ti23z12 | 0 | -0.0090(3) |
| O1x1 | 0.0010(3) | -0.0005(4) |
| O1y1 | 0.0097(3) | 0.0087(4) |
| O1z1 | -0.0027(4) | -0.0053(5) |
| O1x2 | -0.0003(3) | 0.0020(5) |
| O1y2 | -0.0030(4) | -0.0080(6) |
| O1z2 | 0.0025(5) | 0.0039(8) |
| O1x3 | 0 | -0.0027(7) |
| O1y3 | 0 | 0.0065(7) |
| O1z3 | 0 | 0.0006(10) |
| O2x1 | -0.0054(2) | 0.0029(2) |
| O2y1 | -0.0075(3) | 0.0228(3) |
| O2z1 | 0.0036(4) | 0.0020(3) |
| O2x2 | 0.0030(3) | 0.0053(3) |
| O2y2 | 0.0059(4) | -0.0100(4) |
| O2z2 | -0.0020(4) | -0.0050(4) |
| O2x3 | 0 | -0.0039(3) |
| O2y3 | 0 | 0.0057(5) |
| O2z3 | 0 | 0.0048(5) |
| O3x1 | 0.0023(3) | -0.0006(3) |
| O3y1 | 0.0058(3) | 0.0183(3) |
| O3z1 | 0.0134(4) | -0.0023(3) |
| O3x2 | -0.0015(3) | -0.0105(3) |
| O3y2 | 0.0026(4) | -0.0072(4) |
| O3z2 | -0.0050(4) | -0.0024(4) |
| O3x3 | 0 | 0.0085(4) |
| O3y3 | 0 | 0.0039(5) |
| O3z3 | 0 | 0.0050(5) |
Definition of the ADP Fourier series: (Show/hide table) [ Help ]
| Modulation code | Atom site label | Tensor element | Wave vector code |
|---|---|---|---|
| Ca1U111 | Ca1 | U11 | 1 |
| Ca1U221 | Ca1 | U22 | 1 |
| Ca1U331 | Ca1 | U33 | 1 |
| Ca1U121 | Ca1 | U12 | 1 |
| Ca1U131 | Ca1 | U13 | 1 |
| Ca1U231 | Ca1 | U23 | 1 |
| Ca1U112 | Ca1 | U11 | 2 |
| Ca1U222 | Ca1 | U22 | 2 |
| Ca1U332 | Ca1 | U33 | 2 |
| Ca1U122 | Ca1 | U12 | 2 |
| Ca1U132 | Ca1 | U13 | 2 |
| Ca1U232 | Ca1 | U23 | 2 |
ADP Fourier coefficients: (Show/hide table) [ Help ]
| Modulation code | Cosine coefficient | Sine coefficient |
|---|---|---|
| Ca1U111 | 0.0012(3) | 0.0035(3) |
| Ca1U221 | -0.0002(3) | 0.0035(3) |
| Ca1U331 | -0.0010(4) | 0.0035(4) |
| Ca1U121 | 0.0003(4) | -0.0008(4) |
| Ca1U131 | -0.0001(7) | -0.0001(4) |
| Ca1U231 | 0.0008(4) | -0.0015(4) |
| Ca1U112 | 0 | 0.0005(5) |
| Ca1U222 | 0 | 0.0017(4) |
| Ca1U332 | 0 | -0.0020(5) |
| Ca1U122 | 0 | 0.0008(5) |
| Ca1U132 | 0 | -0.0010(6) |
| Ca1U232 | 0 | 0.0001(7) |
Occupation crenel coefficients: (Show/hide table) [ Help ]
| Atom site label | Center (x0) | Width |
|---|---|---|
| Ca1 | 0 | 0.1429 |
| Ca2 | 0.113003(16) | 0.0357 |
| Ca3 | -0.107121(18) | 0.0357 |
| Nb11 | 0 | 0.0714 |
| Ti11 | 0 | 0.0714 |
| Nb12 | 0.0536 | 0.0357 |
| Ti12 | 0.0536 | 0.0357 |
| Nb13 | 0.0893 | 0.0357 |
| Ti13 | 0.0893 | 0.0357 |
| Nb21 | 0 | 0.0714 |
| Ti21 | 0 | 0.0714 |
| Nb22 | 0.0536 | 0.0357 |
| Ti22 | 0.0536 | 0.0357 |
| Nb23 | 0.0893 | 0.0357 |
| Ti23 | 0.0893 | 0.0357 |
| O1 | 0 | 0.2143 |
| O2 | 0 | 0.25 |
| O3 | 0 | 0.25 |